اكتشف الباحثون شكلاً واحداً يبلط المستوى بشكل لا دوري بدون انعكاس

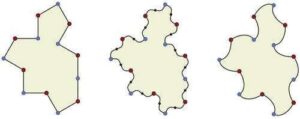
المضلع ذو الـ14 ضلعاً Tile(1,1)، على اليسار، معروف بأنه بلاطة أحادية لا دورية ضعيفة التماثل – بمعنى آخر، إذا كانت التبليطات التي تمزج بين البلاطات غير المنعكسة والمنعكسة محظورة، فإنها تبلط فقط بشكل لا دوري. ومع ذلك، من خلال تعديل حوافها، كما هو موضح في الوسط واليمين، تم إنشاء بلاطات أحادية لا دورية صارمة التماثل تسمى ””أطياف”“ لا تسمح إلا بتبليطات غير دورية. المصدر: جامعة واترلو

اكتشف مؤخراً فريق دولي مكون من أربعة أشخاص، من بينهم الدكتور كريج كابلان أستاذ مدرسة تشيريتون لعلوم الحاسوب، شكلاً واحداً يبلط المستوى – وهو سطح ثنائي الأبعاد لا نهائي – في نمط لا يمكن أبداً جعله يتكرر.

أذهل هذا الاكتشاف علماء الرياضيات وهواة التبليط والجمهور على حد سواء.

الشكل، وهو مضلع ذو 13 ضلعاً أطلقوا عليه اسم ””القبعة”“، معروف لدى علماء الرياضيات باسم البلاطة الأحادية اللادورية أو ””آينشتاين”“، وهي كلمة ألمانية تعني ””حجر واحد”“.

لكن اكتشاف الفريق الأخير رفع المستوى مرة أخرى. لقد وجدوا شكلاً آخر، مرتبطاً بالأول، يلبي تعريفاً أكثر صرامة. أُطلق على الشكل الجديد اسم ””الطيف”“، وهو يبلط المستوى في نمط لا يتكرر أبداً دون استخدام صور مرآوية للشكل. لهذا السبب، أُطلق عليه أيضاً اسم ””آينشتاين مصاص الدماء”“ – وهو شكل يبلط بشكل لا دوري دون الحاجة إلى انعكاسه.

””حلت ورقتنا الأولى مشكلة آينشتاين، ولكن نظراً لأن الشكل يتطلب انعكاساً للتبليط بشكل لا دوري، طرح الناس سؤالاً مشروعاً: هل هناك شكل يمكنه فعل ما تفعله القبعة ولكن بدون انعكاس،”“ يشرح كابلان. ””كان من حسن حظنا أننا وجدنا شكلاً لا يحل هذه المشكلة الفرعية فحسب، بل حلها أيضاً بعد وقت قصير من نشر الورقة الأولى.”“

بالنسبة لعلماء الرياضيات، تعتبر القبعة وصورتها المرآوية شكلاً واحداً، ولكن في العالم المادي يمكن أن تتصرف الأشكال اليسرى واليمنى بشكل مختلف. لا يمكنك، على سبيل المثال، ارتداء قفاز أيمن على يدك اليسرى.

””إذا قمت بتبليط أرضية حمام كبيرة بشكل لا دوري باستخدام بلاط على شكل قبعة تم تزجيجه من جانب واحد، فستحتاج إلى قبعات وصور مرآوية للقبعات،”“ يقول كابلان.

لكن لم يكن هذا الجدل هو الذي حفز الاكتشاف الأخير.

بدأ اكتشاف آينشتاين مصاص الدماء بتأملات ديفيد سميث، وهو فني طباعة متقاعد وهاوي أشكال كما يصف نفسه من يوركشاير، إنجلترا، الذي أدى فضوله قبل أشهر إلى اكتشاف آينشتاين الأصلي.

””أرسل ديف لنا بريداً إلكترونياً بعد يومين من نشر ورقة القبعة عبر الإنترنت ليقول إنه كان يعبث بشكل مرتبط بها وبدا أنه يتصرف بشكل غريب،”“ يقول كابلان. ””يوشياكي أراكي، وهو عالم رياضيات ياباني وفنان معروف يعمل بروح إم سي إيشر، نشر صوراً لـ Tile(1,1) جعلت ديف مهتماً بالنظر إليها بشكل أعمق.”“

نشر يوشياكي سؤالاً مثيراً للاهتمام على تويتر: “تبليط سلحفاة لا دوري مبني على بلاطة أحادية لا دورية جديدة Tile(1, 1.1). في التبليط، يُقال إن حوالي 12.7% من البلاطات منعكسة. اللون الأخضر هو مثال. هناك سلحفاة منعكسة أخرى مخفية في التبليط. من هي المنعكسة؟'”

””حوّل يوشي Tile(1,1) إلى سلاحف ومن الصعب بعض الشيء رؤية السلحفاة المنعكسة الأخرى في تلك الصورة. لكن هذا أثار فضول ديف. ماذا لو قمنا بالتبليط بهذا الشكل ولكن بدون انعكاسات؟ وبينما كان يفعل ذلك، وجد ديف أنه يمكنه بناء تبليطات تتوسع تدريجياً للخارج في نمط لا يتوقف ولا يتكرر.”“

لكن هذا الشكل جاء مع جدل مختلف. كما يشرح كابلان، إذا استخدمت انعكاسات Tile(1,1) فإن النمط يتكرر. بمعنى آخر، إنه دوري. ولكن إذا تم تعديل Tile(1,1) عن طريق استبدال حوافه المستقيمة بمنحنيات، فإنه يصبح آينشتاين مصاص دماء – شكل واحد بدون انعكاس يبلط المستوى اللانهائي في نمط لا يمكن أبداً جعله يتكرر.

السؤال الواضح لعلماء الرياضيات وهواة التبليط هو ما الخطوة التالية؟

””يمكننا طرح العديد من الاختلافات للمشكلة،”“ يقول كابلان. ””الأكثر إثارة للاهتمام، بالنسبة لي على الأقل، هو ما إذا كان يمكن القيام بذلك في الأبعاد الثلاثية. سيكون من الجميل أن يكون لدينا شكل يتكرر بشكل غير دوري في ثلاثة أبعاد. مثل هذه التركيبات أصعب بكثير في التصور، ولكن من الناحية الحسابية ليس من الصعب إثباتها إذا كنا محظوظين بما يكفي للعثور على شكل ثلاثي الأبعاد – متعدد الأشكال – الذي مثل القبعة يبلط فقط بشكل لا دوري.”“

””نظرية التبليط كفرع من الرياضيات جميلة وملموسة وتحتوي على الكثير من المشاكل المثيرة للاهتمام التي يجب حلها. لا يوجد نقص في العمل المتابع الذي يجب القيام به.”“

سيقام مهرجان القبعة، احتفالاً باكتشاف ””القبعة”“، في معهد الرياضيات بجامعة أكسفورد من 20 إلى 21 يوليو. سيتضمن اليوم الأول من الحدث محادثات وورش عمل حول التبليط موجهة للجمهور العام، بينما سيتضمن اليوم الثاني عروضاً تقديمية موجهة لجمهور واسع من الفيزيائيين وعلماء الرياضيات.

لمزيد من هذه الرؤى، قم بتسجيل الدخول إلى موقعنا https://international-maths-challenge.com

تُنسب المقالة إلى جو بيتريك، جامعة واترلو