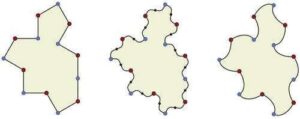
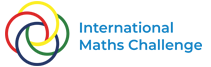左侧的 14 边形 Tile(1,1) 被称为弱手性非周期性单瓦——换句话说,如果禁止混合未反射和反射瓦片的平铺,那么它只能非周期性地平铺。然而,通过修改其边缘,如中心和右侧所示,创建了称为 “spectres” 的严格手性非周期性单瓦,它们只允许非周期性平铺。图片来源:滑铁卢大学
最近,一个由四人组成的国际团队,其中包括切里顿计算机科学学院的 Craig Kaplan 博士,发现了一种可以平铺平面的单一形状——一个无限的二维表面——其图案永远无法重复。
这一发现让数学家、平铺爱好者和公众都为之着迷。
这种形状,一个 13 边形,他们称之为 “the hat”,在数学家眼中被称为非周期性单瓦或 “einstein”,这个德语单词的意思是 “one stone”。
但该团队最近的发现再次提高了标准。他们发现了另一种形状,与第一种形状相关,它符合更严格的定义。这种新形状被称为 “specter”,它以一种永不重复的模式平铺一个平面,而无需使用该形状的镜像。因此,它也被称为 “vampire einstein”——一种无需反射即可非周期性平铺的形状。
“我们的第一篇论文解决了 einstein 问题,但由于该形状需要反射才能非周期性地平铺,人们提出了一个合理的问题:是否存在一种形状可以像 hat 一样做到这一点,但无需反射,” Kaplan 解释说。“我们很幸运地找到了一个不仅解决了这个子问题,而且在第一篇论文之后不久就解决了它的形状。”
对于数学家来说,hat 及其镜像是一个单一的形状,但在物理世界中,左手和右手的形状表现可能不同。例如,你不能在左手上戴右手手套。
“如果你用一面上了釉的 hat 形瓷砖非周期性地铺设一个大型浴室地板,你需要 hat 和 hat 的镜像,” Kaplan 说。
但并非是这种吹毛求疵促成了最近的发现。
vampire einstein 的发现始于 David Smith 的沉思,他是一位退休的印刷技术员,也是一位来自英国约克郡的自称形状爱好者,几个月前他的好奇心促成了最初的 einstein 发现。
“在我们的 hat 论文上线几天后,Dave 给我们发了一封电子邮件,说他一直在摆弄一个相关的形状,这个形状的行为似乎很奇怪,” Kaplan 说。“日本数学家兼著名艺术家 Yoshiaki Araki 的作品具有 MC Escher 的精神,他发布了 Tile(1,1) 的图片,这引起了 Dave 对它的进一步关注。”
Yoshiaki 在 Twitter 上发布了一个有趣的问题:“基于新的非周期性单瓦 Tile(1, 1.1) 的非周期性海龟镶嵌。在镶嵌中,据说大约 12.7% 的瓷砖被反射。绿色的是一个例子。还有一个反射的海龟隐藏在镶嵌中。谁被反射了?”
“Yoshi 将 Tile(1,1) 变成了海龟,并且很难在该图片中看到另一个反射的海龟。但这引起了 Dave 的好奇。如果我们用这种形状平铺,但不进行反射呢?当他这样做时,Dave 发现他可以逐步向外构建平铺,其模式不会停止也不会重复。”
但随后这种形状出现了一个不同的问题。正如 Kaplan 解释的那样,如果你使用 Tile(1,1) 的反射,则该模式会重复。换句话说,它是周期性的。但是,如果通过用曲线替换其直线边缘来修改 Tile(1,1),它就会变成 vampire einstein——一种无需反射即可在永不重复的模式中平铺无限平面的单一形状。
对于数学家和平铺爱好者来说,显而易见的问题是接下来会发生什么?
“我们可以提出许多问题的变体,” Kaplan 说。“至少对我来说,最有趣的是这是否可以在 3D 中完成。如果有一种形状可以在三个维度上非周期性地重复,那就太好了。这种结构更难可视化,但从计算上来说,证明我们是否足够幸运地找到一个三维形状(一种多形体)并不难,就像 hat 一样,它只能非周期性地平铺。”
“平铺理论作为数学的一个分支是美丽的、有形的,并且有很多有趣的问题需要解决。不乏后续工作要做。”
Hatfest 是对 “the Hat” 发现的庆祝活动,将于 7 月 20 日至 21 日在牛津大学数学研究所举行。该活动的第一天将以针对普通观众的关于平铺的讲座和研讨会为特色,而第二天将以针对广泛的物理学家和数学家观众的演讲为特色。
要了解更多此类见解,请登录我们的网站 https://international-maths-challenge.com
本文的作者是滑铁卢大学的 Joe Petrik