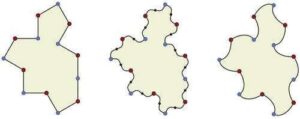
左側的 14 邊形 Tile(1,1) 被稱為弱手性非週期單瓦 — 換句話說,如果禁止混合未反射和反射瓦片的鋪砌,則它僅以非週期性方式鋪砌。 然而,透過修改其邊緣,如中心和右側所示,可以創建稱為「幽靈」的嚴格手性非週期單瓦,這些單瓦僅允許非週期性鋪砌。 圖片來源:滑鐵盧大學
最近,一個由四人組成的國際團隊(包括 Cheriton 電腦科學學院教授 Craig Kaplan 博士)發現了一種單一形狀,可以鋪滿平面(一個無限的二維表面),其圖案永遠無法重複。
這一發現讓數學家、鋪砌愛好者和公眾都為之著迷。
這種形狀,一個 13 邊形,他們稱之為「帽子」,數學家稱之為非週期單瓦或「愛因斯坦」,這個德語詞的意思是「一塊石頭」。
但該團隊最近的發現再次提高了標準。 他們發現了另一種與第一種形狀相關的形狀,它符合更嚴格的定義。 這種被稱為「幽靈」的新形狀,以一種永遠不會重複的模式鋪滿平面,而無需使用該形狀的鏡像。 因此,它也被稱為「吸血鬼愛因斯坦」— 一種無需反射即可非週期性鋪砌的形狀。
「我們的第一篇論文解決了愛因斯坦問題,但由於該形狀需要反射才能進行非週期性鋪砌,因此人們提出了一個合理的問題:是否有一種形狀可以像帽子一樣,但無需反射,」Kaplan 解釋說。 「我們很幸運地找到了一種形狀,它不僅解決了這個子問題,而且在第一篇論文發表後不久就解決了它。」
對於數學家來說,帽子及其鏡像是一個單一的形狀,但在物理世界中,左手和右手的形狀表現可能不同。 例如,你不能在左手上戴右手手套。
「如果你用帽子形狀的瓷磚以非週期性方式鋪砌一個大型浴室地板,這些瓷磚的一面已經上釉,那麼你需要帽子和帽子的鏡像,」Kaplan 說。
但並非這種吹毛求疵促成了最近的發現。
吸血鬼愛因斯坦的發現始於 David Smith 的沉思,他是一位退休的印刷技術員,也是一位來自英國約克郡的自稱形狀愛好者,幾個月前他的好奇心促成了最初的愛因斯坦發現。
「在我們的帽子論文上線幾天后,Dave 給我們發了一封電子郵件,說他一直在玩一種相關的形狀,這種形狀的表現似乎很奇怪,」Kaplan 說。 「日本數學家兼著名藝術家 Yoshiaki Araki 的作品具有 MC Escher 的精神,他發布了 Tile(1,1) 的圖片,這引起了 Dave 的興趣,並進一步研究它。」
Yoshiaki 在 Twitter 上發布了一個有趣的問題:「基於新的非週期單瓦 Tile(1, 1.1) 的非週期海龜鑲嵌。在鑲嵌中,據說大約 12.7% 的瓷磚被反射。綠色的是一個例子。在鑲嵌中還隱藏著另一隻被反射的海龜。誰是被反射的?」
「Yoshi 將 Tile(1,1) 變成了海龜,很難在圖片中看到另一隻被反射的海龜。但這引起了 Dave 的好奇。如果我們用這種形狀鋪砌,但不進行反射呢?當他這樣做時,Dave 發現他可以逐步向外構建鋪砌,其模式不會停止也不會重複。」
但這種形狀帶有不同的吹毛求疵。 正如 Kaplan 解釋的那樣,如果你使用 Tile(1,1) 的反射,則圖案會重複。 換句話說,它是週期性的。 但是,如果通過用曲線替換其直線邊緣來修改 Tile(1,1),它就會變成吸血鬼愛因斯坦 — 一種單一形狀,無需反射即可在永不重複的模式中鋪砌無限平面。
對於數學家和鋪砌愛好者來說,顯而易見的問題是下一步是什麼?
「我們可以提出這個問題的許多變體,」Kaplan 說。 「至少對我來說,最有趣的是這是否可以在 3D 中完成。如果有一種形狀可以在三個維度中非週期性地重複,那就太好了。這樣的結構很難視覺化,但如果我們有幸找到一種三維形狀(一種多形體),像帽子一樣僅以非週期性方式鋪砌,那麼在計算上證明它並不會困難得多。」
「作為數學的一個分支,鋪砌理論是美麗的、有形的,並且有很多有趣的問題需要解決。不乏後續工作要做。」
Hatfest,一個慶祝「帽子」發現的活動,將於 7 月 20 日至 21 日在牛津大學數學研究所舉行。 該活動的第一天將以針對普通觀眾的關於鋪砌的講座和研討會為特色,而第二天將以針對廣泛的物理學家和數學家觀眾的演示為特色。
如需更多此類見解,請登入我們的網站 https://international-maths-challenge.com
本文的作者為滑鐵盧大學的 Joe Petrik