某个氚原子会在某个时间前衰变吗?根据我们目前的科学,关于物理现象的这个问题应该通过从概率分布中抽样来回答,这个过程与旋转轮盘或掷骰子没什么不同。然而,Foundations of Physics 上的一篇论文表明,同样的情况也可能适用于关于数学现象的问题,即使是像“2+2 等于多少?”这样平淡无奇的问题。
SFI 教授、物理学家 David Wolpert 和前 SFI Omidyar 研究员、哲学家兼认知科学家 David Kinney 提出了一个统一的概率框架,用于描述数学、物理宇宙,甚至描述人类如何对两者进行推理。
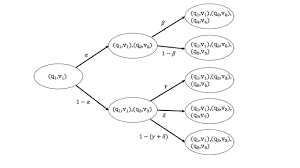
在他们的框架中,数学和科学都被表示为提问和回答问题的过程。给定的数学家或科学家如何回答问题将取决于他们分配给不同答案的概率。在基本形式主义的扩展中,这些相同的概率也决定了数学家或科学家回答这些问题的正确程度。
为了说明这一点,假设你现在回答一个数学问题,而在遥远的未来,一些数学家回答了同样的问题。你答案的正确性取决于你的概率与他们的概率的匹配程度。(在物理学中,你的正确性将涉及物理实验,而不是未来的物理学家。)
从问题选择到给出的答案,随机性渗透到问题-答案过程的每个部分。这导致了所提出的框架的一个重要好处:为科学和数学中的两个常识性捷径提供了一种新颖的、正式的理由——更强烈地相信有多种证据支持的想法,以及更强烈地相信最能解释你已经相信的东西的想法。
要了解更多此类见解,请登录我们的网站 https://international-maths-challenge.com
本文的作者为圣塔菲研究所