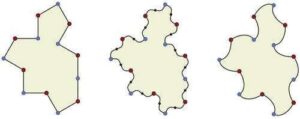
왼쪽에 있는 14면체 다각형 Tile(1,1)은 약한 카이랄 비주기적 모노타일로 알려져 있습니다. 즉, 반사되지 않은 타일과 반사된 타일이 혼합된 타일링이 금지된다면, 이 도형은 비주기적으로만 타일링됩니다. 하지만 중앙과 오른쪽에 보이는 것처럼 가장자리를 수정함으로써, 비주기적 타일링만 허용하는 “스펙터” 라고 불리는 엄격한 카이랄 비주기적 모노타일이 생성됩니다. 출처: 워털루 대학교
최근 체리턴 컴퓨터 과학 대학의 크레이그 카플란 교수도 포함된 4명으로 구성된 국제 연구팀은 무한한 2차원 표면인 평면을 결코 반복되지 않는 패턴으로 타일링하는 단 하나의 도형을 발견했습니다.
이 발견은 수학자, 타일링 애호가, 그리고 일반 대중 모두를 매료시켰습니다.
그들이 “모자” 라고 부르는 이 13면체 다각형은 수학자들에게 비주기적 모노타일 또는 “아인슈타인” 으로 알려져 있는데, 이는 “하나의 돌” 을 의미하는 독일어 단어입니다.
하지만 연구팀의 가장 최근 발견은 다시 한번 수준을 한 단계 더 끌어올렸습니다. 그들은 첫 번째 도형과 관련이 있으면서 훨씬 더 엄격한 정의를 충족하는 또 다른 도형을 발견했습니다. “스펙터” 라고 불리는 이 새로운 도형은 도형의 거울상을 사용하지 않고도 결코 반복되지 않는 패턴으로 평면을 타일링합니다. 이러한 이유로 이 도형은 “뱀파이어 아인슈타인”—즉, 반사를 요구하지 않고 비주기적으로 타일링하는 도형—이라고도 불립니다.
카플란 교수는 설명합니다. “저희의 첫 번째 논문은 아인슈타인 문제를 해결했지만, 그 도형이 비주기적으로 타일링하기 위해 반사를 필요로 했기 때문에 사람들은 정당한 질문을 제기했습니다. ‘모자가 하는 일을 반사 없이 할 수 있는 도형이 있을까?’” “저희는 이 하위 문제를 해결할 뿐만 아니라, 첫 번째 논문이 나온 지 얼마 되지 않아 이 문제를 해결하는 도형을 찾게 된 것이 큰 행운이었습니다.”
수학자들에게는 모자와 그 거울상은 하나의 도형이지만, 물리적인 세계에서는 왼손잡이 도형과 오른손잡이 도형은 다르게 행동할 수 있습니다. 예를 들어, 오른손 장갑을 왼손에 낄 수는 없습니다.
카플란 교수는 말합니다. “만약 한쪽 면이 유약 처리된 모자 모양의 타일로 넓은 욕실 바닥을 비주기적으로 타일링한다면, 모자와 모자의 거울상이 모두 필요할 것입니다.”
하지만 최근 발견을 촉발한 것은 이러한 사소한 논쟁이 아니었습니다.
뱀파이어 아인슈타인의 발견은 몇 달 전 그의 호기심이 원래의 아인슈타인 발견으로 이어졌던 영국 요크셔 출신의 은퇴한 인쇄 기술자이자 스스로를 도형 애호가라고 칭하는 데이비드 스미스의 생각에서 시작되었습니다.
카플란 교수는 말합니다. “저희의 모자 논문이 온라인에 공개된 지 며칠 후, 데이브는 관련 도형을 가지고 놀다가 이상하게 행동하는 것처럼 보였다고 이메일을 보냈습니다.” “MC 에셔의 정신을 이어받은 작품으로 유명한 일본 수학자이자 예술가인 아라키 요시아키가 Tile(1,1)의 사진을 올렸는데, 데이브가 그것을 더 자세히 살펴보는 데 관심을 갖게 되었습니다.”
요시아키는 트위터에 흥미로운 질문을 올렸습니다. “새로운 비주기적 모노타일 Tile(1, 1.1)을 기반으로 한 비주기적 거북이 테셀레이션. 이 타일링에서 약 12.7%의 타일이 반사된다고 합니다. 녹색 타일이 한 예시입니다. 타일링 안에 반사된 거북이가 하나 더 숨어 있습니다. 반사된 것은 누구일까요?”
“요시가 Tile(1,1)을 거북이로 만들었는데, 그 사진에서는 다른 반사된 거북이를 찾기가 좀 어렵습니다. 하지만 데이브는 호기심을 갖게 되었습니다. ‘이 도형으로 타일링하되 반사 없이 하면 어떨까?’ 그렇게 하면서 데이브는 멈추지 않고 반복되지 않는 패턴으로 타일링을 점진적으로 바깥쪽으로 확장해 나갈 수 있다는 것을 발견했습니다.”
하지만 그때 이 도형은 또 다른 문제점을 안고 있었습니다. 카플란 교수가 설명하듯이, Tile(1,1)의 반사된 형태를 사용하면 패턴은 반복됩니다. 다시 말해, 그것은 주기적입니다. 하지만 Tile(1,1)의 직선 가장자리를 곡선으로 대체하여 수정하면, 그것은 뱀파이어 아인슈타인—즉, 반사 없이 무한 평면을 결코 반복되지 않는 패턴으로 타일링하는 단 하나의 도형—이 됩니다.
수학자와 타일링 애호가들에게 명백한 질문은 ‘다음은 무엇인가?’입니다.
카플란 교수는 말합니다. “우리는 이 문제의 다양한 변형을 제시할 수 있습니다.” “적어도 저에게는 가장 흥미로운 점은 이것이 3D로도 가능한지 여부입니다. 3차원에서 비주기적으로 반복되는 도형이 있다면 좋을 것입니다. 그러한 구성은 시각화하기 훨씬 어렵지만, 만약 모자처럼 비주기적으로만 타일링되는 3차원 도형—폴리폼—을 찾을 수 있다면, 계산적으로 증명하는 것이 그렇게 훨씬 더 어렵지는 않을 것입니다.”
“수학의 한 분야로서 타일링 이론은 아름답고, 실질적이며, 해결해야 할 매혹적인 문제들이 많습니다. 앞으로 해야 할 후속 연구는 부족하지 않습니다.”
“모자” 의 발견을 기념하는 햇페스트(Hatfest)는 7월 20일부터 21일까지 옥스퍼드 대학교 수학 연구소에서 개최될 예정입니다. 행사 첫째 날에는 일반 대중을 대상으로 한 타일링 강연과 워크숍이 진행될 예정이며, 둘째 날에는 물리학자와 수학자 등 폭넓은 청중을 대상으로 한 발표가 있을 예정입니다.
더 많은 통찰력을 얻으려면 저희 웹사이트 https://international-maths-challenge.com에 접속하세요.
기사 제공: 워털루 대학교 조 페트릭