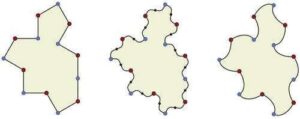
Le polygone à 14 côtés Tile(1,1), à gauche, est connu comme un monotuile apériodique faiblement chiral — en d’autres termes, si les pavages qui mélangent des tuiles non réfléchies et réfléchies sont interdits, alors il ne pave que de manière apériodique. Cependant, en modifiant ses bords, comme montré au centre et à droite, des monotuiles apériodiques strictement chiraux appelés « spectres » sont créés qui n’admettent que des pavages non périodiques. Crédit : Université de Waterloo
Récemment, une équipe internationale de quatre personnes, qui inclut le professeur Dr. Craig Kaplan de l’École d’informatique Cheriton, a découvert une forme unique qui pave le plan — une surface infinie bidimensionnelle — selon un motif qui ne peut jamais être rendu répétitif.
La découverte a fasciné les mathématiciens, les passionnés de pavage et le grand public.
La forme, un polygone à 13 côtés qu’ils ont appelé « le chapeau », est connue des mathématiciens comme un monotuile apériodique ou un « einstein », les mots allemands qui signifient « une pierre ».
Mais la découverte la plus récente de l’équipe a encore relevé la barre. Ils ont trouvé une autre forme, liée à la première, qui répond à une définition encore plus stricte. Surnommée le « spectre », la nouvelle forme pave un plan selon un motif qui ne se répète jamais sans utiliser d’images miroir de la forme. Pour cette raison, elle a aussi été appelée un « einstein vampire » — une forme qui pave de manière apériodique sans nécessiter sa réflexion.
« Notre premier article a résolu le problème d’einstein, mais comme la forme nécessitait une réflexion pour paver de manière apériodique, les gens ont soulevé une question légitime : Existe-t-il une forme qui peut faire ce que fait le chapeau mais sans réflexion », explique Kaplan. « Nous avons eu la chance de trouver une forme qui non seulement résout ce sous-problème, mais l’a aussi résolu si peu de temps après le premier article. »
Pour les mathématiciens, le chapeau et son image miroir constituent une seule forme, mais dans le monde physique, les formes gauches et droites peuvent se comporter différemment. Vous ne pouvez pas, par exemple, porter un gant de la main droite sur votre main gauche.
« Si vous paviez le sol d’une grande salle de bain de manière apériodique avec des tuiles en forme de chapeau qui auraient été émaillées d’un côté, vous auriez besoin de chapeaux et d’images miroir de chapeaux », dit Kaplan.
Mais ce n’est pas cette chicane qui a motivé la découverte récente.
La découverte de l’einstein vampire a commencé avec les réflexions de David Smith, un technicien d’imprimerie retraité et passionné de formes autodidacte du Yorkshire, en Angleterre, dont la curiosité quelques mois plus tôt avait mené à la découverte originale d’einstein.
« Dave nous a envoyé un courriel quelques jours après que notre article sur le chapeau soit mis en ligne pour dire qu’il avait joué avec une forme apparentée qui semblait se comporter étrangement », dit Kaplan. « Yoshiaki Araki, un mathématicien japonais et artiste bien connu dont le travail est dans l’esprit de MC Escher, avait publié des images de Tile(1,1) qui ont intéressé Dave à l’examiner davantage. »
Yoshiaki a posté une question intrigante sur Twitter : « Une tessellation de tortue apériodique basée sur le nouveau monotuile apériodique Tile(1, 1.1). Dans le pavage, il est dit qu’environ 12,7 % des tuiles sont réfléchies. La verte en est un exemple. Une tortue réfléchie de plus est cachée dans le pavage. Qui est la réfléchie ? »
« Yoshi avait transformé Tile(1,1) en tortues et il est un peu difficile de voir l’autre tortue réfléchie dans cette image. Mais cela a rendu Dave curieux. Et si nous pavions avec cette forme mais sans réflexions ? En faisant cela, Dave a trouvé qu’il pouvait construire des pavages progressivement vers l’extérieur selon un motif qui ne s’arrêtait pas et ne se répétait pas. »
Mais alors cette forme est venue avec une chicane différente. Comme l’explique Kaplan, si vous utilisez des réflexions de Tile(1,1), le motif se répète effectivement. En d’autres termes, il est périodique. Mais si Tile(1,1) est modifié en remplaçant ses bords droits par des courbes, il devient un einstein vampire — une forme unique qui sans réflexion pave le plan infini selon un motif qui ne peut jamais être rendu répétitif.
La question évidente pour les mathématiciens et les passionnés de pavage est : quelle est la suite ?
« Nous pouvons poser de nombreuses variations du problème », dit Kaplan. « La plus intéressante, pour moi du moins, est de savoir si cela peut être fait en 3D. Il serait agréable d’avoir une forme qui se répète de manière non périodique en trois dimensions. De telles constructions sont beaucoup plus difficiles à visualiser, mais informatiquement ce n’est pas tellement plus difficile à prouver si nous avons la chance de trouver une forme tridimensionnelle — une polyforme — qui comme le chapeau ne pave que de manière apériodique. »
« La théorie du pavage en tant que branche des mathématiques est belle, tangible, et a beaucoup de problèmes fascinants à résoudre. Il n’y a pas de pénurie de travaux de suivi à faire. »
Hatfest, une célébration de la découverte du « Chapeau », aura lieu à l’Institut mathématique de l’Université d’Oxford du 20 au 21 juillet. Le premier jour de l’événement présentera des conférences et des ateliers sur le pavage destinés à un public profane, tandis que le second présentera des présentations destinées à un large public de physiciens et de mathématiciens.
Pour plus de telles perspectives, connectez-vous à notre site web https://international-maths-challenge.com
Crédit de l’article donné à Joe Petrik, Université de Waterloo