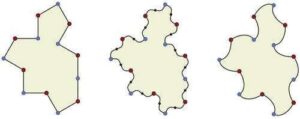
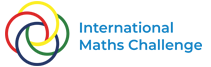Das 14-seitige Polygon Tile(1,1) links ist als schwach chirale aperiodische Monokachel bekannt – das heißt, wenn Parkettierungen, die ungespiegelte und gespiegelte Kacheln mischen, verboten sind, dann parkettiert es nur aperiodisch. Durch Modifizierung seiner Kanten, wie in der Mitte und rechts gezeigt, werden jedoch streng chirale aperiodische Monokacheln namens „Spectres“ erzeugt, die nur nicht-periodische Parkettierungen zulassen. Quelle: University of Waterloo
Kürzlich entdeckte ein internationales Viererteam, dem Professor Dr. Craig Kaplan von der Cheriton School of Computer Science angehört, eine einzelne Form, die die Ebene – eine unendliche, zweidimensionale Oberfläche – in einem Muster parkettiert, das sich niemals wiederholen lässt.
Die Entdeckung faszinierte Mathematiker, Parkettierungs-Enthusiasten und die Öffentlichkeit gleichermaßen.
Die Form, ein 13-seitiges Polygon, das sie „den Hut“ nannten, ist Mathematikern als aperiodische Monokachel oder als „Einstein“ bekannt, die deutschen Wörter, die „ein Stein“ bedeuten.
Doch die jüngste Entdeckung des Teams hat die Messlatte erneut höher gelegt. Sie fanden eine weitere Form, die mit der ersten verwandt ist und eine noch strengere Definition erfüllt. Die neue Form, die den Namen „Specter“ erhielt, parkettiert eine Ebene in einem Muster, das sich niemals wiederholt, ohne die Verwendung von Spiegelbildern der Form. Aus diesem Grund wurde sie auch als „Vampir-Einstein“ bezeichnet – eine Form, die aperiodisch parkettiert, ohne ihre Spiegelung zu benötigen.
„„Unser erstes Paper löste das Einstein-Problem, aber da die Form eine Spiegelung benötigte, um aperiodisch zu parkettieren, stellten die Leute eine berechtigte Frage: Gibt es eine Form, die das kann, was der Hut kann, aber ohne Spiegelung?“ erklärt Kaplan. „„Es war unser Glück, dass wir eine Form fanden, die nicht nur dieses Teilproblem löst, sondern es auch so kurz nach dem ersten Paper gelöst hat.“
Für Mathematiker sind der Hut und sein Spiegelbild eine einzige Form, aber in der physischen Welt können sich linkshändige und rechtshändige Formen unterschiedlich verhalten. Man kann zum Beispiel keinen rechtshändigen Handschuh an der linken Hand tragen.
„„Wenn man einen großen Badezimmerboden aperiodisch mit hut-förmigen Kacheln parkettieren würde, die auf einer Seite glasiert waren, bräuchte man Hüte und Spiegelbilder von Hüten,“ sagt Kaplan.
Doch es war nicht dieser Einwand, der die jüngste Entdeckung motivierte.
Die Entdeckung des Vampir-Einsteins begann mit den Überlegungen von David Smith, einem pensionierten Drucktechniker und selbsternannten Formen-Liebhaber aus Yorkshire, England, dessen Neugier Monate zuvor zur ursprünglichen Einstein-Entdeckung geführt hatte.
„„Dave mailte uns ein paar Tage, nachdem unser Hut-Paper online gegangen war, um zu sagen, dass er mit einer verwandten Form herumgespielt hatte, die sich seltsam zu verhalten schien,“ sagt Kaplan. „„Yoshiaki Araki, ein japanischer Mathematiker und bekannter Künstler, dessen Werk im Geiste von MC Escher steht, hatte Bilder von Tile(1,1) gepostet, die Dave dazu brachten, sich näher damit zu beschäftigen.“
Yoshiaki stellte eine faszinierende Frage auf Twitter: „Eine aperiodische Schildkröten-Tessellation basierend auf der neuen aperiodischen Monokachel Tile(1, 1.1). In der Parkettierung heißt es, dass etwa 12,7 % der Kacheln gespiegelt sind. Die grüne ist ein Beispiel. Eine weitere gespiegelte Schildkröte ist in der Parkettierung versteckt. Wer ist die gespiegelte?“
„„Yoshi hatte Tile(1,1) in Schildkröten verwandelt, und es ist etwas schwer, die andere gespiegelte Schildkröte auf diesem Bild zu sehen. Aber es machte Dave neugierig. Was wäre, wenn wir mit dieser Form parkettieren, aber ohne Spiegelungen? Als er das tat, stellte Dave fest, dass er Parkettierungen schrittweise nach außen in einem Muster aufbauen konnte, das nicht aufhörte und sich nicht wiederholte.“
Doch dann kam diese Form mit einem anderen Einwand. Wie Kaplan erklärt, wiederholt sich das Muster, wenn man Spiegelungen von Tile(1,1) verwendet. Mit anderen Worten, es ist periodisch. Doch wenn Tile(1,1) modifiziert wird, indem seine geraden Kanten durch Kurven ersetzt werden, wird es zu einem Vampir-Einstein – einer einzelnen Form, die ohne Spiegelung die unendliche Ebene in einem Muster parkettiert, das sich niemals wiederholen lässt.
Die offensichtliche Frage für Mathematiker und Parkettierungs-Enthusiasten ist: Was kommt als Nächstes?
„„Wir können viele Variationen des Problems stellen,“ sagt Kaplan. „„Das Interessanteste, zumindest für mich, ist, ob dies in 3D möglich ist. Es wäre schön, eine Form zu haben, die sich in drei Dimensionen nicht-periodisch wiederholt. Solche Konstruktionen sind viel schwieriger zu visualisieren, aber rechnerisch ist es nicht viel schwieriger zu beweisen, sollten wir das Glück haben, eine dreidimensionale Form – ein Polyform – zu finden, die wie der Hut nur aperiodisch parkettiert.“
„„Die Parkettierungstheorie als Zweig der Mathematik ist schön, greifbar und hat viele faszinierende Probleme zu lösen. Es gibt keinen Mangel an weiterer Arbeit zu tun.“
Hatfest, eine Feier der Entdeckung von „dem Hut,“ findet vom 20. bis 21. Juli am Mathematischen Institut der Universität Oxford statt. Der erste Tag der Veranstaltung bietet Vorträge und Workshops zum Thema Parkettierung, die sich an ein Laienpublikum richten, während der zweite Tag Präsentationen für ein breites Publikum von Physikern und Mathematikern bietet.
Für weitere Einblicke dieser Art besuchen Sie unsere Website https://international-maths-challenge.com
Artikel von Joe Petrik, University of Waterloo