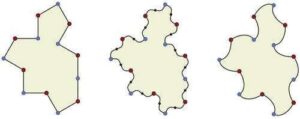
El polígono de 14 lados Tile(1,1), a la izquierda, se conoce como un monotile aperiódico débilmente quiral; en otras palabras, si se prohíben los mosaicos que mezclan tiles no reflejados y reflejados, entonces solo cubre de forma aperiódica. Sin embargo, al modificar sus bordes, como se muestra en el centro y a la derecha, se crean monotiles aperiódicos estrictamente quirales llamados “espectros” que admiten solo mosaicos no periódicos. Crédito: Universidad de Waterloo
Recientemente, un equipo internacional de cuatro personas, que incluye al profesor de la Escuela de Ciencias de la Computación de Cheriton, el Dr. Craig Kaplan, descubrió una forma única que cubre el plano (una superficie bidimensional infinita) en un patrón que nunca se puede hacer que se repita.
El descubrimiento cautivó a matemáticos, entusiastas de los mosaicos y al público por igual.
La forma, un polígono de 13 lados que llamaron “el sombrero”, es conocida por los matemáticos como un monotile aperiódico o un “einstein”, las palabras alemanas que significan “una piedra”.
Pero el descubrimiento más reciente del equipo ha subido el listón una vez más. Encontraron otra forma, relacionada con la primera, que cumple una definición aún más estricta. Apodada el “espectro”, la nueva forma cubre un plano en un patrón que nunca se repite sin el uso de imágenes especulares de la forma. Por esta razón, también se le ha llamado “einstein vampiro”: una forma que cubre aperiódicamente sin necesidad de su reflejo.
“Nuestro primer artículo resolvió el problema de einstein, pero como la forma requería reflexión para cubrir aperiódicamente, la gente planteó una pregunta legítima: ¿Existe una forma que pueda hacer lo que hace el sombrero pero sin reflexión?”, explica Kaplan. “Fue nuestra buena fortuna que encontramos una forma que no solo resuelve este subproblema, sino que también lo resolvió tan pronto después del primer artículo.”
Para los matemáticos, el sombrero y su imagen especular son una sola forma, pero en el mundo físico las formas zurdas y diestras pueden comportarse de manera diferente. No puedes, por ejemplo, usar un guante diestro en tu mano izquierda.
“Si cubrieras un gran suelo de baño aperiódicamente con tiles en forma de sombrero que hubieran sido esmaltados en un lado, necesitarías sombreros e imágenes especulares de sombreros”, dice Kaplan.
Pero no fue esta objeción lo que motivó el reciente descubrimiento.
El descubrimiento del einstein vampiro comenzó con las reflexiones de David Smith, un técnico de impresión jubilado y autodenominado aficionado a las formas de Yorkshire, Inglaterra, cuya curiosidad meses antes condujo al descubrimiento original de einstein.
“Dave nos envió un correo electrónico un par de días después de que nuestro artículo sobre el sombrero se publicara en línea para decir que había estado jugando con una forma relacionada que parecía comportarse de manera extraña”, dice Kaplan. “Yoshiaki Araki, un matemático japonés y artista conocido cuyo trabajo está en el espíritu de MC Escher, había publicado imágenes de Tile(1,1) que hicieron que Dave se interesara en mirarlo más a fondo.”
Yoshiaki publicó una pregunta intrigante en Twitter: “Una teselación de tortugas aperiódicas basada en el nuevo monotile aperiódico Tile(1, 1.1). En la teselación, se dice que alrededor del 12,7% de los tiles se reflejan. El verde es una instancia. Una tortuga más reflejada está oculta en la teselación. ¿Quién es el reflejado?'”
“Yoshi había convertido Tile(1,1) en tortugas y es un poco difícil ver la otra tortuga reflejada en esa imagen. Pero despertó la curiosidad de Dave. ¿Qué pasa si cubrimos con esta forma pero sin reflejos? Al hacer eso, Dave descubrió que podía construir mosaicos progresivamente hacia afuera en un patrón que no se detenía y no se repetía.”
Pero entonces esta forma vino con una objeción diferente. Como explica Kaplan, si usas reflejos de Tile(1,1) el patrón sí se repite. En otras palabras, es periódico. Pero si Tile(1,1) se modifica reemplazando sus bordes rectos con curvas, se convierte en un einstein vampiro: una forma única que sin reflejo cubre el plano infinito en un patrón que nunca se puede hacer que se repita.
La pregunta obvia para los matemáticos y los entusiastas de los mosaicos es ¿qué sigue?
“Podemos plantear muchas variaciones del problema”, dice Kaplan. “Lo más interesante, al menos para mí, es si esto se puede hacer en 3D. Sería bueno tener una forma que se repita no periódicamente en tres dimensiones. Tales construcciones son mucho más difíciles de visualizar, pero computacionalmente no es mucho más difícil de probar si tuviéramos la suerte de encontrar una forma tridimensional, un poliforma, que al igual que el sombrero solo cubre aperiódicamente.”
“La teoría de los mosaicos como rama de las matemáticas es hermosa, tangible y tiene muchos problemas fascinantes por resolver. No hay escasez de trabajo de seguimiento por hacer.”
Hatfest, una celebración del descubrimiento de “el Sombrero”, tendrá lugar en el Instituto Matemático de la Universidad de Oxford del 20 al 21 de julio. El primer día del evento contará con charlas y talleres sobre mosaicos dirigidos a un público no especializado, mientras que el segundo contará con presentaciones dirigidas a un público amplio de físicos y matemáticos.
Para obtener más información, inicie sesión en nuestro sitio web https://international-maths-challenge.com
Crédito del artículo otorgado a Joe Petrik, Universidad de Waterloo